ยูเนียน อินเตอร์เซกชัน
คอมพลีเมนต์
ยูเนียน อินเตอร์เซกชัน
และคอมพลีเมนต์ของเซต เป็นส่วนหนึ่งของการกระทำระหว่างเซต
เรานิยมเขียนออกมาในสองรูปแบบด้วยกันคือแบบสมการ และแผนภาพเวนน์-ออยเลอร์
เราลองมาดูกันครับว่ายูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต
เป็นอย่างไรพร้อมตัวอย่าง
ยูเนียน
(Union)
ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต
B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B
สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B
ตัวอย่างเช่น
A ={1,2,3}
B= {3,4,5}
∴ A ∪ B = {1,2,3,4,5}
เราสามารถเขียนการยูเนี่ยนลงในแผนภาพได้ดังนี้
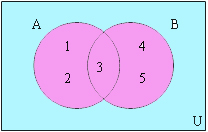
อินเตอร์เซกชัน
(Intersection)
อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต
A อินเตอร์เซกชันเซต B คือ
เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B
สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B
ตัวอย่างเช่น
A ={1,2,3}
B = {3,4,5}
∴ A ∩ B =
{3}
เราสามารถเขียนการอินเตอร์เซกชันลงในแผนภาพได้ดังนี้
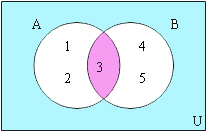
คอมพลีเมนต์
(Complements)
คอมพลีเมนต์ (Complements) มีนิยามคือ
ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต
A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์
A’
ตัวอย่างเช่น
U = {1,2,3,4,5}
A ={1,2,3}
∴ A’ =
{4,5}
เราสามารถเขียนการคอมพลีเมนต์ของเซตลงในแผนภาพได้ดังนี้
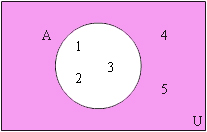
ไม่มีความคิดเห็น:
แสดงความคิดเห็น